Abstract
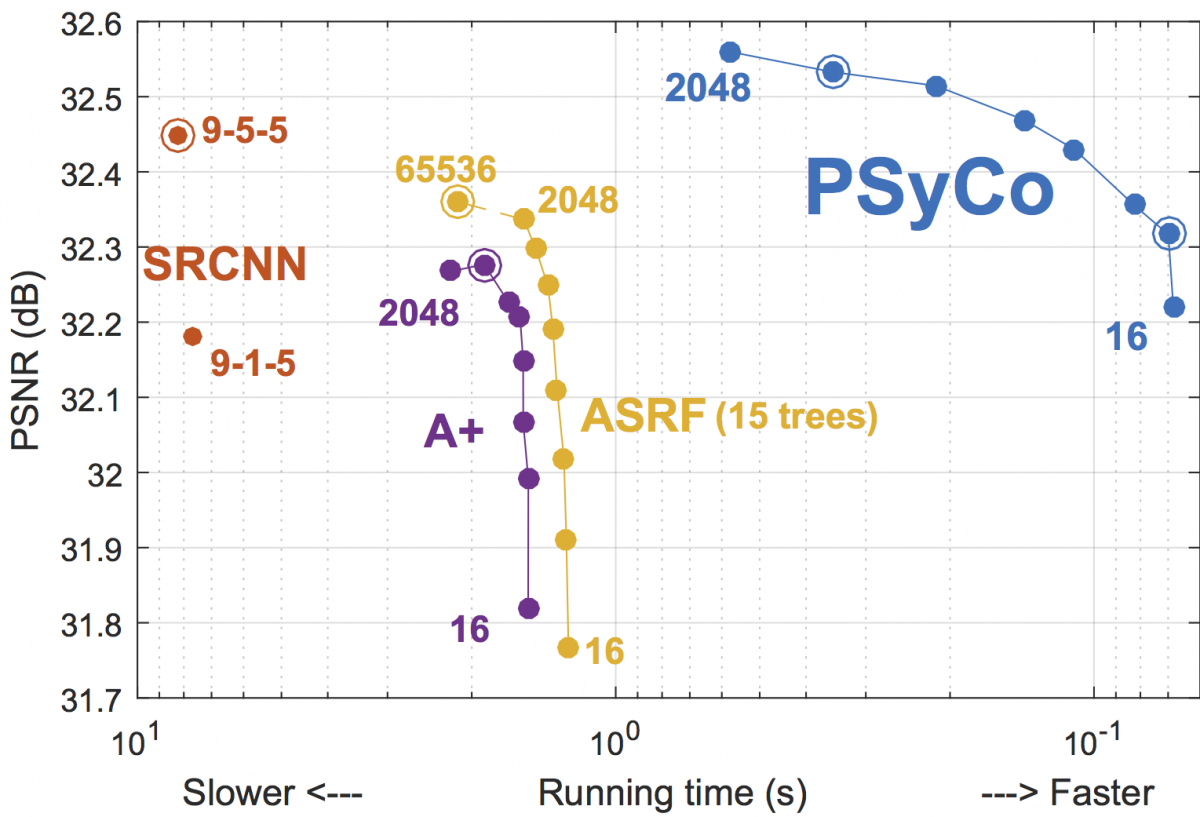
The main challenge in Super Resolution (SR) is to discover the mapping between the low- and high-resolution manifolds of image patches, a complex ill-posed problem which has recently been addressed through piecewise linear regression with promising results. In this paper we present a novel regression-based SR algorithm that benefits from an extended knowledge of the structure of both manifolds. We propose a transform that collapses the 16 variations induced from the dihedral group of transforms (i.e. rotations, vertical and horizontal reflections) and antipodality (i.e. di- ametrically opposed points in the unitary sphere) into a single primitive. The key idea of our transform is to study the different dihedral elements as a group of symmetries within the high-dimensional manifold. We obtain the respective set of mirror-symmetry axes by means of a frequency analysis of the dihedral elements, and we use them to collapse the redundant variability through a modified symmetry distance. The experimental validation of our algorithm shows the effectiveness of our approach, which obtains competitive quality with a dictionary of as little as 32 atoms (reducing other methods’ dictionaries by at least a factor of 32) and further pushing the state-of-the-art with a 1024 atoms dictionary.
