Abstract
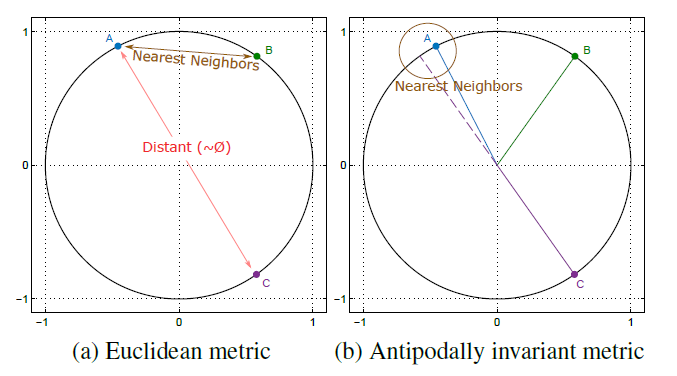
IIn this paper we study the characteristics of the metrics best suited for the piecewise regression algorithms, in which comparisons are usually made between normalized vectors that lie on the unitary hypersphere. Even though Euclidean distance has been widely used for this purpose, it is suboptimal since it does not handle antipodal points (i.e. diametrically opposite points) properly. Therefore, we propose the usage of antipodally invariant metrics and introduce the Half Hypersphere Confinement (HHC), a fast alternative to Multidimensional Scaling (MDS) that allows to map antipodally invariant distances in the Euclidean space with very little approximation error. The performance of our method, which we named HHC Regression (HHCR), applied to Super-Resolution (SR) improves both in quality (PSNR) and it is faster than any other state-of-the-art method. Additionally, under an application-agnostic interpretation of our regression framework, we also test our algorithm for denoising and depth upscaling with promising results.
